Most of us have heard the phrase that there are “lies, damned lies, and statistics”, but I’d venture to say that, outside of academic circles, few actually know just how true that is. As a statistics professor, I am always astonished by the complete lack of statistical competence among those who use statistics regularly. At best, these instances represent a complete ignorance of statistical interpretations; at worst they highlight the ability of biased actors to shape debates by serving tortured or incomplete data to the masses. This post is just the first in a statistical deep-dive series in which we will explore how statistics are used to confuse and mislead (intentionally or not). We will pull real world examples and discuss the flaws with the data and analytics used. These examples will range from the controversial, to the downright bizarre, so buckle up because it’s about to get nerdy up in here. If you want to be notified each time I drop a new post, please considered subscribing (below). Let’s start with perhaps my favorite such example: the relationship between correlation and causation.
Issue #1: Correlation does not imply causation
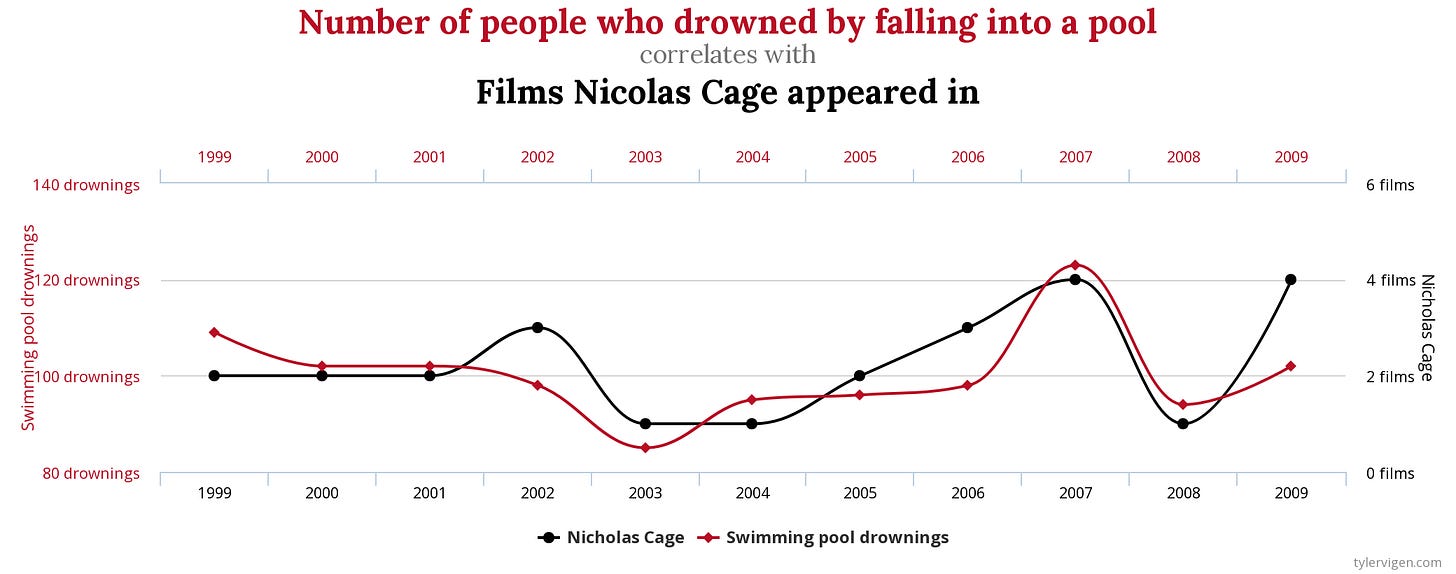
There is a correlation between the number of films that Nicholas Cage stars in, and the number of people who drown by falling in a pool on any given year (or at least there was until 2009):
Given that (according to IMDB.com) Nicholas Cage has 7 films upcoming over the next year or two, suffice it to say: we are screwed. Cover your pools… We’ll try swimming again in 2025. How could Cage be so reckless?! Or wait… maybe directors are troubled by instances of drowning, and decide to soothe the soul of a troubled world by rushing America’s favorite flat-affected actor (sorry Keanu) to the big screen. Or, perhaps, this is what is known as a spurious correlation. In order to understand what a spurious correlation is, I think it may be helpful for us to first understand what a correlation is.
A correlation is simply a modeled relationship between two variables (in this case the number of people who drowned by falling into a pool, and the number of films that Nicholas Cage appeared in). When we talk about correlations there are two main components you need to consider: first, is it positive or negative? Positive and negative are not value judgements, but rather indications of what one variable does in relationship to another. A positive correlation means that as one variable increases, so too does the other variable (or vice versa). One classic example of a positive correlation would be temperature and ice cream sales. As temperature outside rises, so too does that number of ice cream sales. A negative correlation, on the other hand, means that as one variable increases, the other decreases (and vice versa). If we instead substituted hot chocolate sales in the example above we would have a negative correlation: as temperature increases, hot cocoa sales decrease. In both of these cases we can feel comfortable making assumptions about causality (it is most likely the temperature which is driving the sales of hot cocoa and ice cream). But sometimes two things may be correlated, because they are both affected by a third factor. For example, there is a positive correlation between ice cream sales and shark attacks. Now, it is probably not the case that people eat ice cream only for sharks to be drawn to the newly sweet victims, nor is it the case that people overcome the trauma of shark attacks with dippin’ dots. Likely, both of these variables are linked to the third variable of temperature. As it gets warmer more people will want ice cream, but more people will also be inclined to go into the ocean thereby increasing the likelihood that someone has a shark encounter. However, even in this case we have identified a likely cause of the relationship. The second major issue to consider is the strength of the correlation. However, as with all good Nicholas Cage movies, this second point will be left as a cliff hanger, to be addressed in a future movie.. I mean blog post. This leads back to the conversation about spurious correlations.
Spurious correlations are those for which there is likely no causal effect, nor shared relationship to a tertiary variable. In the case of drownings and Nicholas Cage movies, it is likely just a coincidence that these two things are related. Now some may say that knowing this correlation still provides predictive value: even if Nicholas Cage isn’t causing people to drown, we can better predict the number of drownings which will occur simply by knowing the number of Nicholas Cage movies. While this is an enticing argument, it is fundamentally flawed. If there is no shared causal mechanism, there is nothing to keep these two variables from becoming completely decoupled. At some point, the coincidence will end, and you will be left sounding like an insane person warning all community pools to close because the star of National Treasure (turns out he wasn’t in DaVinci Code… Thanks Mike!) is slated to have a particularly busy year next year.
So you may be asking yourself: how did the website TylerVigen.com even discover that there was such a correlation (check out that website for a lot of other great spurious correlations)? I mean what a freaking obscure relationship to even consider! Well the reality is that with enough data, you will find things that correlate, regardless of whether they share a causal mechanism. If I had to bet, I would guess that Tyler collected data for hundreds (if not thousands) of different variables, and checked for correlations between all of those variables. This may seem like a contrived example, but the reality is that this type of research occurs all the time, with results that are less obvious.
Partly out of necessity, many medical studies run massive correlational studies to evaluate how things like certain diets or behaviors can predict health outcomes. These studies involve evaluating tens, and sometimes hundreds, of correlations to see where there may be relationships for future exploration. Often times the authors of such studies offer appropriate words of caution that are promptly crumbled up and thrown in the trashcan by well-intentioned (but statistically illiterate) journalists looking for an eye-catching story. Here are two of my favorite examples that I have personally seen:
Now let’s think about this one for a second. What could be the causal mechanism? Perhaps big cities have better healthcare? Perhaps they have better access to cheaper high-quality food? Maybe there’s something about the energy or social dynamics in a city that make you live longer? But one thing we can say is that the mere fact that you’re in a big city in California does not cause you to live longer. There is likely a shared mechanism somewhere in there, but if we were to hold everything else constant (i.e. same healthcare, same food, same social situations, same weather, etc.) does the fact that you live in a big city in California somehow affect your longevity? No. This is a great example of the real causal mechanism being obscured by a flashy headline.
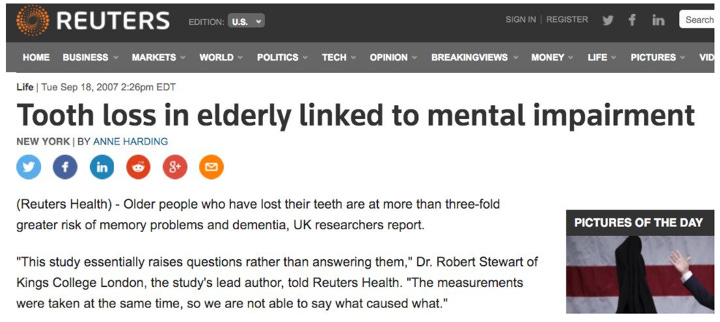
Ahh yes, we all know that childhood song: “The head bone’s connected to the brain bone, the brain bone’s connected to the tooth bone…” My favorite part of this story is the quote from Dr. Stewart at the end of the second paragraph: “… so we are not able to say what caused what.” That may be true, but I can tell you what certainly did NOT directly cause dementia… losing your teeth. One may be surprised to learn that we don’t store memories in our teeth. While it is entirely possible that losing ones teeth indirectly increases the risk of dementia (perhaps through changing diets, bacterial infection, etc.) to say that simply losing ones teeth could potentially cause dementia starts with a profound misunderstanding of human cognition, and ends with a questionable understanding of human anatomy. Again, this is not to say this is a spurious correlation (although it may be), but Reuters makes a causal claim from correlational data in their first sentence: “Older people who have lost their teeth are at more than three-fold greater risk of memory problems and dementia”. Perhaps those with dementia are less likely to remember oral hygiene and therefore begin losing their teeth. This would be a testable causal claim. But I cannot stress this enough: your brain is not stored in your teeth and therefore losing your teeth cannot directly lead to memory problems.
Before I end, however, I think it is important to address the reality which is so often missed by those with a baseline statistical understanding.
Issue #2: Correlation does not imply causation, but it does not rule it out
This may seem obvious to most, but there is a startling propensity for those who have had their heads submerged in the cold waters of a statistics class (thanks Nicholas Cage…) to believe that because correlation does not equal causation, there being a correlation provides evidence that there is no causal relationship. I have found myself crosswise with many who are happy to recite “correlation does not equal causation” when faced with correlational data. I am proud of them for understanding this, but it does not mean that the possibility of a causal relationship shouldn’t be explored.
Let’s look at a personal example that I am all too familiar with after the holidays. An hour or two after I eat a lot of sweets, I feel like crap. This is correlational (and anecdotal). While it is true that you could come up with a convincing causal argument in both directions, and it would be illogical to derive causation from this correlational data alone, the mere fact that it is correlational should not preclude us from considering the possible causal mechanisms (like sugar causes inflammation) . To simply say “correlation does not equal causation” and then carry on eating sweets like I’m a Willy Wonka character would be asinine. These correlational findings are sometimes spurious, but are also sometimes illustrative of a causal mechanism (whether direct or not). This is where exciting science happens; experimentation can help inform the directionality of causation, while ruling out competing hypotheses. If something is correlational, don’t take it as causal, but also don’t forbid yourself from thinking about the possible causal relationship simply because it is correlational. Much in the same way that introductory Psychology students love to diagnose their friends with various disorders, introductory statisticians love to over apply principles like “correlation does not equal causation” at the expense of effortful consideration of the data.
I hope you’ve enjoyed this first dive into the world of statistics. If you haven’t… consider this correlational rather than causal, and collect data of your own by sharing this post with others and see how bored they get by reading it as well. Then share some of my other posts (NateT.Substack.com) and see if their boredom correlates with length of the post. I guess what I’m asking you to do is like, comment, subscribe, and share this post with others. It helps me know what you may be interested in reading, in the future. Now enjoy my favorite nerdy comic strip:



Great pieces of knowledge
“*Why* statistics lie: they never provide a detailed enough picture.”